CUDA简明介绍

随着AI的兴起，老黄的计算卡一卡难求，在深度学习领域老黄已经几乎事实上达到了垄断的地位。而让老黄成为AI领域那个“卖铲子”的正是CUDA，或者说是围绕CUDA诞生的一系列软件生态。

今天就用CUDA实现一个矩阵乘法来简单介绍一下CUDA是如何让GPU突破摩尔定律的以及为什么在AI训练中是如此重要。

CUDA是什么

CUDA全称Compute Unified Device Architecture，是老黄推出的API，方便开发者调用NVIDIA GPU用来进行大规模并行计算。

老黄在Clang编译器的基础上拓展开发了针对CUDA的编译器NVCC，所以NVCC支持大部分C/C++语法特性同时支持针对CUDA的拓展语法。

如何搭建CUDA编程环境

由于NVIDIA与开源社区一向水火不容，所以导致N卡在Linux的兼容性不说完美无缺至少也是丝毫没有，当然这两年由于NVIDIA的数据中心业务水涨船高，老黄也逐渐开源了部分GPU驱动相比于以前已经是好很多了。但是目前来说体验最好的还是用wsl2搭配vscode，不需要折腾驱动，几乎是一键安装，同时NVIDIA也提供了docker镜像方便部署维护，具体可以看上一篇配置wsl2的文章。

CUDA实现矩阵乘法

计算机架构

计算流程

在使用CUDA编程前，我们需要对计算机架构需要有一个了解。

一般来说计算机计算，遵循如下流程

但是当GPU加入进来后的异构计算流程则有一定的区别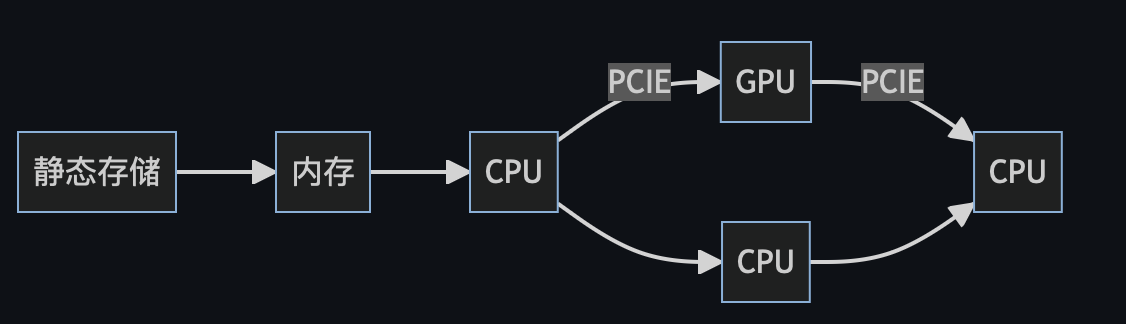在程序运行过程中可以理解为CPU与GPU是异步的，两者通过PCIE通道通信，CPU调用kernel函数后后并不会等待GPU计算结束再继续而是直接继续运行。

GPU架构

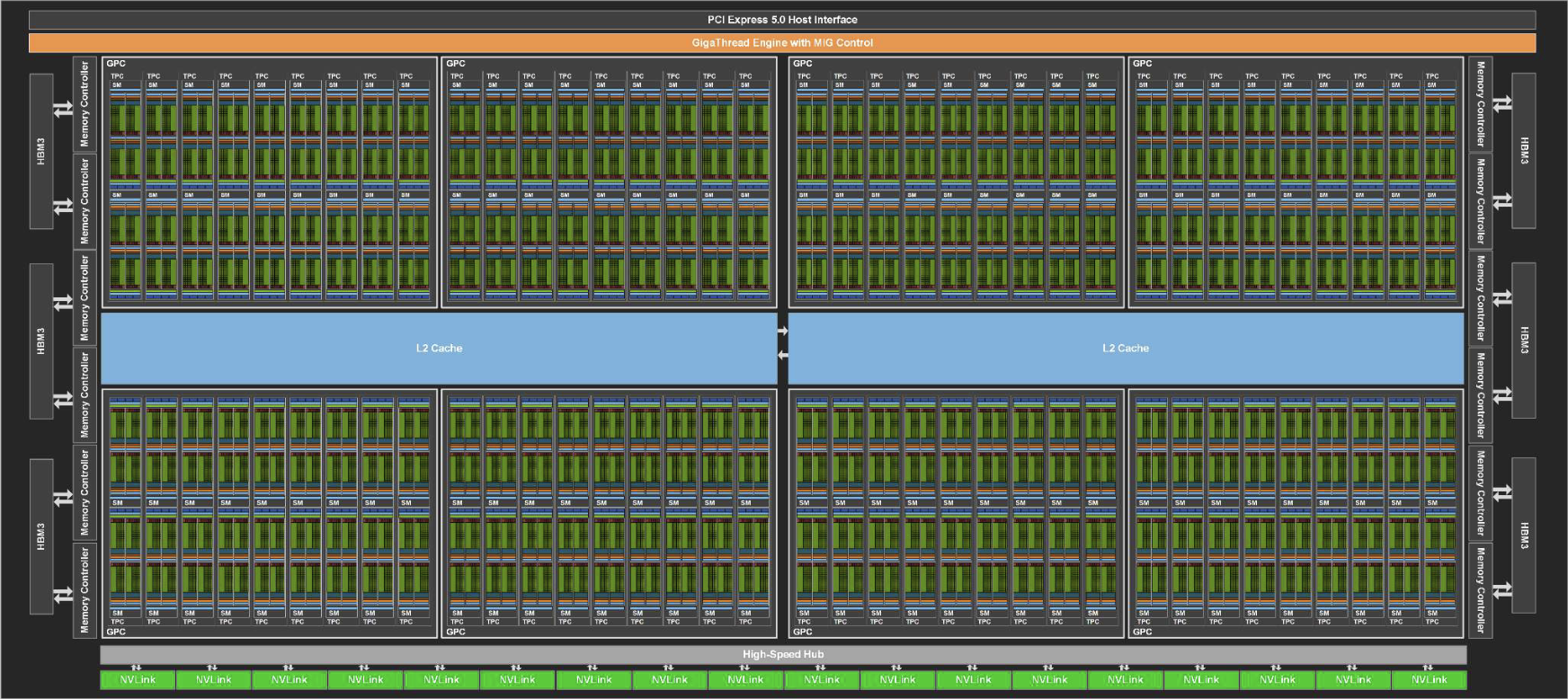H100 我们这里简单介绍一下GPU的架构，上图是H100的架构图。整个H100有8组GPC，每组GPC有9组TPC，每组TPC又有两组SM，而每组SM又有144个CUDA Tensor，共有18432个CUDA Tensor以及两组24MB的L2缓存。同时由于H100是计算专用卡，所以老黄只留了一组光栅单元，打游戏是基本没戏了。

这里每个CUDA Tensor都可以看成是一个CPU核心，但是相比于CPU核心CUDA Tensor不能做复杂的逻辑运算，适合做大规模的并行计算，尤其是适合做矩阵运算。

代码实现

我这里使用CUDA C/C++来实现矩阵的乘法。

1
2


#define MATRIX_SIZE_ROW 32
#define MATRIX_SIZE_COL 32

我们首先定义一下矩阵的大小。

接着用malloc分配一下内存以及利用随机函数给矩阵赋值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


float *a, *b, *c;             // Host matrices

a = (float *)malloc(sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW);
b = (float *)malloc(sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW);
c = (float *)malloc(sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW);

FILE *filea = fopen("matrix_a.txt", "w");
FILE *fileb = fopen("matrix_b.txt", "w");

for (int i = 0; i < MATRIX_SIZE_ROW * MATRIX_SIZE_COL; ++i)
{

    a[i] = (float)(rand() % 10);
    b[i] = (float)(rand() % 10);
    fprintf(filea, "%lf ", a[i]);
    fprintf(fileb, "%lf ", b[i]);
   if (i % MATRIX_SIZE_COL == 0 && i!=0)        {
        fprintf(filea, "\n");
        fprintf(fileb, "\n");
    }
}

这里我把矩阵数值保存到文本中，方便查看。

由于我们需要将host即主机上的数据复制到device即GPU上，所以我们也需要在GPU上分配内存

1
2
3
4
5
6
7
8


float *dev_a, *dev_b, *dev_c; // Device matrices
    // Allocate memory for device matrices
cudaMalloc((void **)&dev_a, sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW);
cudaMalloc((void **)&dev_b, sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW);
cudaMalloc((void **)&dev_c, sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW);
    // Copy host matrices to device matrices
cudaMemcpy(dev_a, a, sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW, cudaMemcpyHostToDevice);
cudaMemcpy(dev_b, b, sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW, cudaMemcpyHostToDevice);

这里用到了CUDA C/C++两个API

cudaMalloc用来在GPU上分配内存cudaMalloc(*ptr,size)
cudaMemcpy用来将host上的内存数据复制到device中

接着我们就需要写kernel函数了，即在device上运行的函数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


// CUDA kernel function to multiply matrices
__global__ void matrixMul(float *a, float *b, float *c, int matrix_size_row, int matrix_size_col)
{

    int row = threadIdx.y + blockIdx.y * blockDim.y;
    int col = threadIdx.x + blockIdx.x * blockDim.x;

    if (row < matrix_size_row && col < matrix_size_col) {
        float sum = 0.0f;

        for (int i = 0; i < matrix_size_col; ++i) {
            sum += a[row * matrix_size_col + i] * b[i * matrix_size_col+ col];
        }

        c[row * matrix_size_col + col] = sum;
    }
}

这里有几个要点

这里的__global__是CUDA C/C++的拓展语法，表明函数是在GPU上执行的，相对的还有__host__和__device__关键词，分别表CPU调用函数(这里__host__一般不显示声明)以及在__global__函数中调用host函数。
重要的一点所有的kernel函数都必须要用void即没有返回值。
与常规的计算流程不同，CUDA并行计算是将对矩阵的索引变为对CUDA线程的索引，这极大的加速了矩阵的计算。

接着我们需要为kernel函数手动分配线程数

1
2
3
4
5


dim3 blockDim(MATRIX_SIZE_COL, MATRIX_SIZE_ROW);
dim3 gridDim((MATRIX_SIZE_COL + blockDim.x - 1) / blockDim.x, (MATRIX_SIZE_ROW + blockDim.y - 1) / blockDim.y);

    // Launch kernel to multiply matrices
matrixMul<<<gridDim, blockDim>>>(dev_a, dev_b, dev_c, MATRIX_SIZE_ROW, MATRIX_SIZE_COL);

这里同样用到了拓展语法分别是dim3数据类型以及<<<gridDim, blockDim>>>

dim3是用来保存分配线程数的数据类型，这里要简单介绍一下CUDA的线程概念，分别是grid、block以及thread，每个grid中可以包含$N_x \times N_y \times N_z$个block同样每个block也可以包含$X \times Y \times Z$个线程，这样我们需要对每个线程进行索引，简单来说就可以想象成将一个二维的矩阵映射到一维进行索引。同时也要注意，在进行索引时不能超出所分配的线程数，否则会发生越界。
<<<gridDim, blockDim>>>这个拓展语法则相对好理解的多，即对matrixMul这个函数分配了对应的线程数。

最后当GPU计算完成，我们还需要将GPU的计算结果同步到CPU中（养成释放内存的好习惯

1
2
3
4
5
6
7
8


cudaMemcpy(c, dev_c, sizeof(float) * MATRIX_SIZE_COL * MATRIX_SIZE_ROW, cudaMemcpyDeviceToHost);

free(a);
free(b);
free(c);
cudaFree(dev_a);
cudaFree(dev_b);
cudaFree(dev_c);

这里同样是利用cudaMemcpy这个函数，将device的数据复制到host中，这里并没有显示的用cudaDeviceSynchronize这个API让CPU等待GPU计算完成再计算，cudaMemcpy隐含了同步的操作。

至此我们已经完成了利用CUDA实现矩阵乘法的流程。如果想看完整代码可以移步我的代码仓库

总结

利用CUDA编程的整体思路还是想当固定的，即为device分配内存，将host数据拷贝到device中，device计算，完成后将device计算结果拷贝到host，最后释放内存。

当然本文写的也是相当简化的一个步骤，CUDA编程相当复杂涉及到很多计算机架构和GPU硬件的知识，比如在涉及到需要经常读取的数据我们就需要用__share__关键词将数据存储到GPU的共享内存，同样在并行求和时常用的reduce算法涉及到数据在线程与线程间归并以及数据竞争的问题。

CUDA编程相较于传统CPU的串行计算有很大的不同，需要我们用不同的视角看问题，同时看到利用CUDA进行并行计算获得远超CPU串行计算的性能时，获得的成就感还是相当让人兴奋的。